gradientSpect

Calculate the gradient using a Fourier spectral method.

Syntax

fx = gradient(f, dx)
fx = gradient(f, dx, [], deriv_order)
fn = gradient(f, dn, dim)
fn = gradient(f, dn, dim, deriv_order)
[fx, fy] = gradient(f, dn)
[fx, fy] = gradient(f, dn, [], deriv_order)
[fx, fy, fz, ...] = gradient(f, dn)
[fx, fy, fz, ...] = gradient(f, dn, [], deriv_order)

Description

gradientSpect calculates the gradient of an n-dimensional input matrix using the Fourier collocation spectral method. The gradient for singleton dimensions is returned as 0.

A 1D example:

% compute gradient of a 2 period sinusoid
x = pi/20:pi/20:4*pi;
y = sin(x);
dydx = gradientSpect(y, pi/20);

% plot gradient and error compared to analytical solution
subplot(2, 1, 1);
plot(x, cos(x), 'k-', x, dydx, 'bx');
axis tight;
title('dy/dx');
subplot(2, 1, 2);
plot(x, cos(x) - dydx, 'k-');
axis tight;
title('Relative Error');

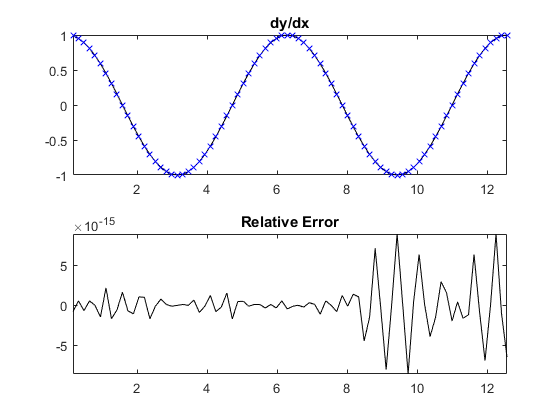
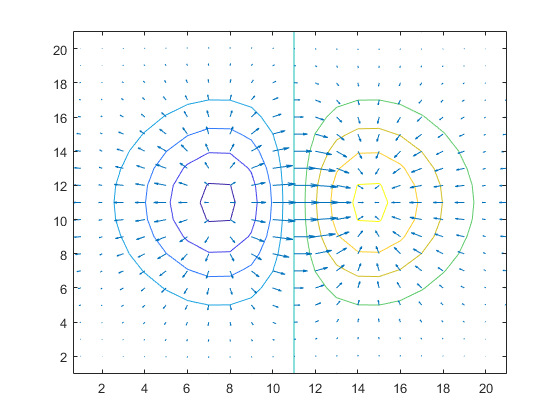
A modification of the example given with the MATLAB gradient function (x and y are reversed):

% generate input and compute gradient
[x, y] = meshgrid(-2:.2:2, -2:.2:2);
z = x .* exp(-x.^2 - y.^2);
[px, py] = gradientSpect(z, [.2, .2]);

% plot
figure;
contour(z)
hold on;
quiver(py, px);
hold off;

Inputs

f	matrix or vector to find the gradient of
dn	array of values for the grid point spacing in each dimension. If a value for dim is given, dn is the spacing in dimension dim.

Optional Inputs

dim	optional input to specify a single dimension over which to compute the gradient for n-dimension input functions
deriv_order	order of the derivative to compute, e.g., use 1 to compute df/dx, 2 to compute df^2/dx^2, etc. (default = 1)

Outputs

fx, fy, ...

gradient in the each dimension, where x corresponds to dim = 1, y corresponds to dim = 2 etc.

See Also

getFDMatrix, gradientFD