makeCartSphericalSegment

Create evenly distributed Cartesian points covering a spherical segment.

Syntax

segment = makeCartSphericalSegment(bowl_pos, radius, inner_diameter, outer_diameter, focus_pos, num_points)
segment = makeCartSphericalSegment(bowl_pos, radius, inner_diameter, outer_diameter, focus_pos, num_points, plot_bowl)

Description

makeCartSphericalSegment makeCartSphericalSegment creates a 3 x num_points array of the Cartesian coordinates of points evenly distributed over the surface of a spherical segment. This function is closely related to makeCartBowl, however, only a segment of the bowl is used (equivalent to an annulus if the bowl was a disc).

The points are calculated using Fermat's spiral. The position of the segment is set by bowl_pos, which corresponds to the center of the rear surface of the bowl from which the annulus is derived. The orientation of the annulus is set by focus_pos, which corresponds to any point on the axis of the annulus (note, this must not be equal to bowl_pos). It is assumed that the solid angle of the bowl from which the annulus is derived is equal to or less than 2*pi steradians. If the radius is set to inf, an annular disc is generated.

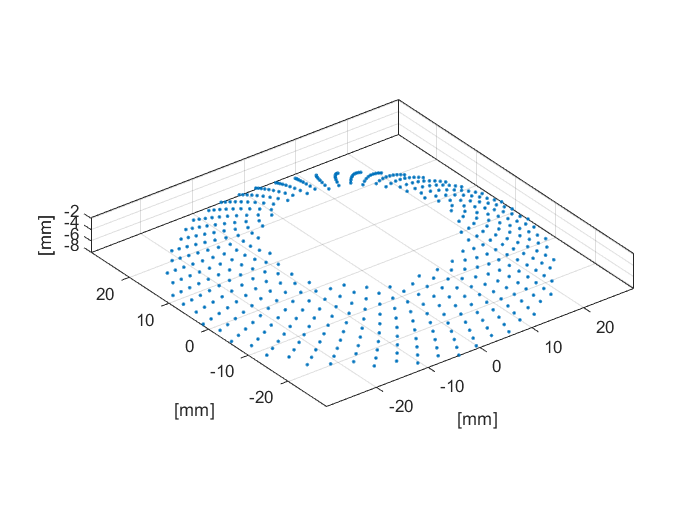
The 3D plot that is displayed after calling makeCartSphericalSegment([0, 0, 0], 60e-3, 30e-3, 60e-3, [0, 0, -1], 500, true); is given below.

Inputs

bowl_pos	Cartesian position of the centre of the rear surface of the underlying bowl on which the spherical segment lies given as a three element vector [bx, by, bz] [m]
radius	Radius of curvature of the underlying bowl [m]
inner_diameter	Inner aperture diameter of the spherical segment [m]
outer_diameter	Outer aperture diameter of the spherical segment [m]
focus_pos	Any point on the beam axis of the underlying bowl given as a three element vector [fx, fy, fz] [m]
num_points	Number of points on the spherical segment

Optional Inputs

plot_bowl	Boolean controlling whether the Cartesian points are plotted (default = false)
num_points_inner	If constructing an annular array with contiguous elements (no kerf), the positions of the points will not exactly match makeCartBowl, as each element has no knowledge of the number of points on the internal elements. To force the points to match, specify the total number of points used on all annular segments internal to the current one.

Outputs

points

3 x num_points array of Cartesian coordinates

See Also

makeCartBowl