.php xmlns="http://www.w3.org/1999/.php"> - k-Wave MATLAB Toolbox
k-Wave Toolbox

focusedBowlONeil

Compute O'Neil's solution for focused bowl transducer.

Syntax

[p_axial, p_lateral] = focusedBowlONeil(radius, diameter, velocity, frequency, sound_speed, density, axial_position, lateral_position);
[p_axial, p_lateral, p_axial_complex] = focusedBowlONeil(radius, diameter, velocity, frequency, sound_speed, density, axial_position, lateral_position);

Description

focusedBowlONeil calculates O'Neil's solution (O'Neil, H. Theory of focusing radiators. J. Acoust. Soc. Am., 21(5), 516-526, 1949) for the axial and lateral pressure amplitude generated by a focused bowl transducer when uniformly driven by a continuous wave sinusoid at a given frequency and normal surface velocity.

The solution is evaluated at the positions along the beam axis given by axial_position (where 0 corresponds to the transducer surface), and lateral positions through the geometric focus given by lateral_position (where 0 corresponds to the beam axis). To return only the axial or lateral pressure, set the either axial_position or lateral_position to [].

Note, O'Neil's formulae are derived under the assumptions of the Rayleigh integral, which are valid when the transducer diameter is large compared to both the transducer height and the acoustic wavelength.

Example:

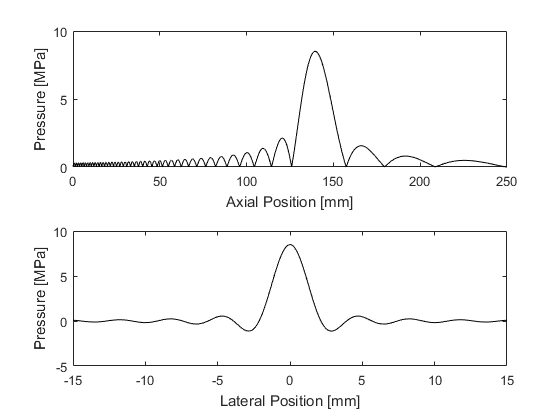
% define transducer parameters
radius      = 140e-3;   % [m]
diameter    = 120e-3;   % [m]
velocity    = 100e-3;   % [m/s]
frequency   = 1e6;      % [Hz]
sound_speed = 1500;     % [m/s]
density     = 1000;     % [kg/m^3]

% define position vectors
axial_position   = 0:1e-4:250e-3;       % [m]
lateral_position = -15e-3:1e-4:15e-3;   % [m]

% evaluate pressure
[p_axial, p_lateral] = focusedBowlONeil(radius, diameter, velocity, ...
    frequency, sound_speed, density, axial_position, lateral_position);

% plot
figure;
subplot(2, 1, 1);
plot(axial_position .* 1e3, p_axial .* 1e-6, 'k-');
xlabel('Axial Position [mm]');
ylabel('Pressure [MPa]');
subplot(2, 1, 2);
plot(lateral_position .* 1e3, p_lateral .* 1e-6, 'k-');
xlabel('Lateral Position [mm]');
ylabel('Pressure [MPa]');

Inputs

radius transducer radius of curvature [m]
diameter diameter of the circular transducer aperture [m]
velocity normal surface velocity [m/s]
frequency driving frequency [Hz]
sound_speed speed of sound in the propagating medium [m/s]
density density in the propagating medium [kg/m^3]
axial_position vector of positions along the beam axis where the pressure amplitude is calculated [m]
lateral_position vector of positions along the lateral direction where the pressure amplitude is calculated [m]

Outputs

p_axial pressure amplitude at the positions specified by axial_position [Pa]
p_lateral pressure amplitude at the positions specified by lateral_position [Pa]
p_axial_complex complex pressure amplitude at the positions specified by axial_position [Pa]

See Also

focusedAnnulusONeil, mendousse
<.php>