mendousse

Compute Mendousse's solution for nonlinear wave propagation in viscous media.

Syntax

p_mendousse = mendousse(x, t, source_freq, p0, c0, rho0, BonA, alpha_0)

Description

mendousse calculates the propagation of a monofrequency plane wave source in a thermoviscous medium with absorption given by alpha_0*f^2. The solution is taken from Eq. (264) in Chapter 4 of Nonlinear Acoustics by Hamilton and Blackstock (2008). The infinite sum is adaptively truncated when the moving average of the previous five sum terms is smaller than a predefined convergence percentage (0.01 percent by default). An example of using the function is given below.

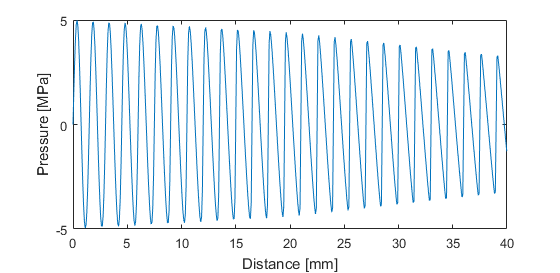
% define the properties used in the simulation
source_freq = 1e6;      % [Hz]
p0 = 5e6;               % [Pa]
c0 = 1500;              % [m/s]
rho0 = 1000;            % [kg/m^3]
BonA = 12;
alpha_0 = 0.5;          % [dB/(MHz^2 cm)]
x = 0:75e-6:40e-3;      % [m]
t = x ./ c0;            % [s]

% compute solution
p_mendousse = mendousse(x, t, source_freq, p0, c0, rho0, BonA, alpha_0);

% plot
figure;
plot(x * 1e3, p_mendousse * 1e-6);
ylabel('Pressure [MPa]');
xlabel('Distance [mm]');
scaleFig(1, 0.65);

Inputs

x	position [m]
t	time [s]
source_freq	frequency of plane wave [Hz]
p0	source pressure [Pa]
c0	medium sound speed [m/s]
rho0	medium density [kg/m^3]
BonA	nonlinearity parameter B/A
alpha_0	absorption coefficient [dB/(MHz^2 cm)]

Outputs

p_mendousse

calculated pressure field [Pa]

Examples

• Modelling Nonlinear Wave Propagation

See Also

focusedBowlONeil